Reply-To: sweetser@alum.mit.edu
Subject: A submission to "Contemporary electrodynamics"
Date: Sun, 30 Sep 2001 22:45:05 -0400
From: Doug B Sweetser
Hello Prof. Dvoeglazov:
This email is in reply to a call for papers to the newsgroup sci.physics.research for a special issue of "Annales de la Foundation Louis de Broglie". The title of my work is "There is no place like home: Looking for a metric equation for gravity within the structure of the Maxwell equations." I hope you find it as much fun to read as it has been to think about and write.
To prevent complications that transmission of attachments sometimes brings, I have included 2 text files at the end of this email. The first is a LaTeX file generated with a program called lyx. Following that is a reference file used by BibTeX. If you have any trouble generating the postscript file, please tell me. kpathsea version 3.3.1 is not generating any errors for me on this file.
Thanks,
doug sweetser
%% LyX 1.1 created this file. For more info, see http://www.lyx.org/. %% Do not edit unless you really know what you are doing. \documentclass[american]{article} \usepackage[T1]{fontenc} \usepackage[latin1]{inputenc} \usepackage{amsmath} \usepackage{babel} \usepackage{amssymb} \makeatletter %%%%%%%%%%%%%%%%%%%%%%%%%%%%%% LyX specific LaTeX commands. \providecommand{\LyX}{L\kern-.1667em\lower.25em\hbox{Y}\kern-.125emX\@} %%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Textclass specific LaTeX commands. \newcommand{\lyxaddress}[1]{ \par {\raggedright #1 \vspace{1.4em} \noindent\par} } %%%%%%%%%%%%%%%%%%%%%%%%%%%%%% User specified LaTeX commands. \bibdata{references.bib} \bibliographystyle{plain} \makeatother \begin{document} \title{There is no place like home: Looking for a metric equation for gravity within the structure of the Maxwell equations} \author{Douglas B. Sweetser} \maketitle \lyxaddress{1340 Commonwealth Ave. Apt. 7, Allston, MA 02134} \date{\today} \begin{abstract} The Maxwell equations written in the Lorenz gauge are known, at least mathematically, to have four modes of transmission: two transverse modes for electrodynamics, a longitudinal, and a scalar mode. The probabilities of the last two modes cancel each other out for photons in a vacuum, but that does not have to be the case for a nonhomogeneous equation. One scalar potential solution to the equations of motion is found, the inverse of an interval between two events squared. The force field created by the potential is constructed by comparison with the classical Newtonian field. The Lagrangian \( L=-J^{\mu }A_{\mu }-\frac{1}{2}(\partial ^{\mu }A^{\nu })(\partial _{\mu }A_{\nu }) \) can contribute to the scalar mode, but still forms the Maxwell equations in the Lorenz gauge. A relativistic force equation is proposed, created by the product of charge, normalized force field, and 4-velocity: \( \frac{\partial mU^{\mu }}{\partial \tau }=kq\frac{\partial ^{\mu }A^{\nu }}{|A|}U_{\nu } \). The solution to the force equation using the inverse square interval potential is found. Eliminating the constants generates a metric equation, \( (\partial \tau )^{2}=e^{-2\frac{GM}{c^{2}\tau }}(\partial t)^{2}-e^{2\frac{GM}{c^{2}\tau }}(\partial \overrightarrow{R})^{2} \), where \( \tau \) is a lightlike interval with almost the same magnitude as the radius \( R \) of separation between source and test masses. For a weak gravitational field, the metric will pass the same tests as the Schwarzschild metric of general relativity. The two metrics differ for higher order terms, which makes the proposed metric distinct and testable experimentally. A constant-velocity solution exists for the gravitational force equation for a system with an exponentially-decaying mass distribution. The dark matter hypothesis is not needed to explain the constant-velocity profiles seen for some galaxies. The proposal may also have implications for classical big bang theory. \end{abstract} \section{An opportunity for gravity within the Maxwell equations} The Maxwell equations can be quantized in a manifestly covariant form by fixing the gauge.\cite{gupta1950} The starting point is the 4-potential \( A^{\mu } \). There are four modes of transmission for photons corresponding to the four degrees of freedom: two transverse, one scalar, and one longitudinal. Gupta calculated that for photons in a vacuum, the probability of the scalar mode cancels that of the longitudinal mode, so both are virtual. He notes that this does not alway have to be the case for the nonhomogeneous Maxwell equations, which is the focus of this work. My hypothesis is that a dominant scalar mode for the Maxwell equations in the Lorenz gauge is gravity. The hypothesis makes several predictions even at this preliminary stage. First, the math of gravity and electromagnetism should be similar but not identical. The inverse square form of Newton's law of gravity was a direct inspiration for Coulomb's law. Gravity should be more symmetric than electromagnetism because the mode is scalar, instead of transverse. The second rank field strength tensor in general relativity is symmetric while the analogous tensor for the electromagnetic field is antisymmetric. Since the mode of gravity is orthogonal to electromagnetism, the charges can be likewise, so there will be no simple relationship between gravitational charge (mass) and electric charge. Gravitational waves in general relativity are transverse, so this proposal is distinct from general relativity. Nature exploits all the math available, so it is unreasonable to suppose that the scalar mode is never used for anything. Whatever phenomenon exploits the scalar mode must be similar, but just as important as electromagnetism. Gravity is a natural candidate. An algebraic road will be constructed starting from a solution to the Maxwell equations in the Lorenz gauge to a curved metric. Many of the steps will be justified by the need to be consistent with Newton's law of gravity in the classical limit. The reward of this work is a metric which is similar enough to the Schwarzschild metric of general relativity to agree with all the experimental results to post-Newtonian accuracy, yet differs for higher order terms. Thus the proposal can be confirmed or refuted by more precise tests of the metric. The second major prediction concerns the velocity profile of spiral galaxies. For a mass distribution that decays exponentially, the equations of motion for the scalar mode predict a stable and flat velocity profile with increasing radius. This eliminates the need for the dark matter hypothesis. \section{A gravitational field inside Maxwell} Newton's classical gravitational law arises from a scalar potential. Here is the scalar field equation: \begin{equation} \label{poisson} \nabla ^{2}\phi =4\pi G\rho . \end{equation} For the case of a vacuum, when \( \rho =0 \), this is known as the Laplace equation. For a spherically symmetric source, one solution is: \begin{equation} \label{potential} \phi =-\frac{GM}{\sqrt{x^{2}+y^{2}+z^{2}}}. \end{equation} The problem with the field equation is that the Laplace operator does not have a time differential. Any change in in the mass density propagates at infinite speed, in conflict with special relativity.\cite[Chapter 7]{misner1970} One way to derive the field equations of general relativity involves making Newton's law of gravity consistent with the finite speed of light.\cite{kraichnan1955} A way to repair the field equations is to use the D'Alembertian operator, which is four dimensional. That expression is identical to the \( A^{0} \) component of the Maxwell equations in the Lorenz gauge: \begin{equation} \label{max_in_lorena_gauge} \Box ^{2}A^{\mu }=4\pi kJ^{\mu }. \end{equation} If one is studying scalar (or possibly longitudinal) modes, \( J^{\mu } \) is the mass density. If one is working with transverse modes, \( J^{\mu } \) is the electric charge density. Since the modes are orthogonal, the sources can be also. To be consistent with the classic scalar potential yet still be relativistic, the potential must have \( x^{2} \), \( y^{2} \), \( z^{2} \), and \( t^{2} \). This suggests a particular solution to the field equations (Eq. \ref{max_in_lorena_gauge}): \begin{equation} \label{1/taupotential} A^{\mu }=(\frac{1}{c^{2}t^{2}-x^{2}-y^{2}-z^{2}},0,0,0). \end{equation} This potential is interesting for several reasons. It is the inverse of the Lorentz-invariant interval squared. Like mass, the 4-potential will not be altered by a change in an inertial reference frame. The interval between any two events will contribute to the potential. General relativity applies to any form of energy, including gravitational field energy. A potential that embraces every interval may have a broad enough scope to do the work of gravity. The potential also has serious problems. Classical gravity depends on an inverse square force field, not an inverse square potential. Taking the derivative of the potential puts a forth power of the interval in the denominator. At this point, I could stop and say that this potential has nothing to do with gravity because it has the wrong dependence on distance. An alternative is to look for an algebraic way to repair the problem. This is the type of approach used by the early workers in quantum mechanics like de Broglie, and will be adopted here. The equations of motion (Eq. \ref{max_in_lorena_gauge}) can be normalized to the magnitude of the 4-potential: \begin{equation} \label{normalized_max} \frac{\Box ^{2}A^{\mu }}{|A|}=4\pi kJ^{\mu }. \end{equation} Since the magnitude of the potential is the inverse interval squared, the resulting equation has only an interval squared in the denominator. An interval is not necessarily the same as the distance R between the source and test mass used in the classical theory. However, I can impose a selection rule that in the classical limit, the only events that contribute to the potential are those that are timelike separated between the source and the test masses. It takes a timelike interval to know that the source is a distance R away. Action-at-a-distance respects the speed of light as it must. \section{Search for the source mass} Where is the source mass in the potential? All that has been discussed so far is an interval, a distance, nothing about mass. An idea from general relativity will be borrowed, that mass can be treated geometrically if multiplied by the constants \( \frac{G}{c^{2}} \). The distance between the Earth and the Sun is approximately \( 1.5x10^{11}m \), while the Sun's mass expressed in units of distance, \( \frac{G\mathrm{M}_{Sun}}{c^{2}} \), is \( 1.5x10^{3}m \), eight orders of magnitude smaller. The overall length of the interval will not be changed noticeably if the spatial separation and the Sun's mass expressed as a distance are summed. However, the force field is the derivative of the potential, and any change in position in spacetime will have a far greater effect proportionally on the smaller geometric mass than the spatial separation. Make the following change of variables: \begin{eqnarray} t & \rightarrow & t'=A+\frac{GM}{2c^{2}A}t\nonumber \\ \overrightarrow{R} & \rightarrow & \overrightarrow{R}'=\overrightarrow{B}+\frac{GM}{2c^{2}|\overrightarrow{B}|}\overrightarrow{R},\label{small_change} \end{eqnarray} where \( A \) and \( \overrightarrow{B} \) are locally constants such that \( \tau ^{2}\cong A^{2}-\overrightarrow{B}^{2} \). The change of variables is valid locally, but not globally, since it breaks down for arbitrarily long time or distance away. General relativity is also valid locally and not globally. The derivative of the normalized interval squared is approximately: \begin{eqnarray} \frac{1}{|\frac{1}{\tau ^{2}}|}\frac{\partial \frac{1}{\tau ^{2}}}{\partial t} & \cong & -\frac{GM}{c^{2}\tau ^{2}}\nonumber \\ \frac{1}{|\frac{1}{\tau ^{2}}|}\overrightarrow{\nabla }\frac{1}{\tau ^{2}} & \cong & \frac{GM}{c^{2}\tau ^{2}}\widehat{R}.\label{derpotential} \end{eqnarray} This should look familiar, remembering that the magnitude of \( \tau ^{2} \) is the same as \( R^{2} \), differing only by the geometric mass of the source. \section{A Lagrangian for four modes} Gupta wanted to quantize the Maxwell equations using a form that was manifestly covariant in its explicit treatment of time and space. He fixed the gauge with this Lagrangian: \begin{equation} \label{gupta_Lagrangian} L=-J^{\mu }A_{\mu }-\frac{1}{2}(\partial ^{\mu }A_{\mu })^{2}-\frac{1}{4}(\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu })(\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }). \end{equation} The equations of motion for this Lagrangian are the Maxwell equations in the Lorenz gauge (Eq. \ref{max_in_lorena_gauge}). The problem with the Lagrangian is that the field strength tensor is antisymmetric. Due to the zeros along the diagonal, it cannot contribute directly to a scalar mode. What is needed is a Lagrangian that could contribute directly to the scalar mode but still have the same equation of motion. Here is such a Lagrangian: \begin{equation} \label{4modelagrangian} L=-J^{\mu }A_{\mu }-\frac{1}{2}(\partial ^{\mu }A^{\nu })(\partial _{\mu }A_{\nu }). \end{equation} This is not as miraculous as it might first appear. It is the first of four terms generated in the contraction of the electromagnetic field strength tensor. In essence, I have chosen not to discard information, which is what happens in making the field strength tensor antisymmetric. The one remaining modification is to normalize both the Lagrangian and equations of motion to the size of the potential. \section{From a 4-force to a metric} A relativistic 4-force is the change in momentum with respect to the interval. The covariant force law is similar in form to the one for electromagnetism except that the second rank tensor is asymmetric and normalized: \begin{equation} \label{4-force} F=\frac{\partial p}{\partial \tau }=m\frac{\partial U^{\mu }}{\partial \tau }+U^{\mu }\frac{\partial m}{\partial \tau }=kq\frac{\partial ^{\mu }A^{\nu }}{|A|}U_{\nu }. \end{equation} In the first application of the force law, assume the derivative of the mass with respect to the interval is zero. For the scalar mode, assume the charge \( q \) is the gravitational test mass. Experiments have demonstrated that gravitational and inertial masses are equal.\cite{will1993} The inverse interval squared potential leads to the following equation of motion: \begin{equation} \label{classical_force_law} (\frac{\partial ^{2}t}{\partial \tau ^{2}}+\frac{GM}{c^{2}\tau ^{2}}\frac{\partial t}{\partial \tau },\frac{\partial ^{2}\overrightarrow{R}}{\partial \tau ^{2}}-\frac{GM}{c^{2}\tau ^{2}}\frac{\partial \overrightarrow{R}}{\partial \tau })=(0,\overrightarrow{0}). \end{equation} Solve this second-order differential equation for the spacetime position: \begin{eqnarray} t & = & c_{1}(\tau e^{\frac{GM}{c^{2}\tau }}-\frac{GM}{c^{2}}Ei(\frac{GM}{c^{2}\tau }))+c_{2}\nonumber \\ \overrightarrow{R} & = & \overrightarrow{C}_{1}(\tau e^{-\frac{GM}{c^{2}\tau }}+\frac{GM}{c^{2}}Ei(-\frac{GM}{c^{2}\tau }))+\overrightarrow{C}_{2},\label{solution} \end{eqnarray} where Ei is the exponential integral, \( Ei(t)=\int ^{t}_{-\infty }\frac{e^{t}}{t}dt \). The exponential integral plays a role in quantum mechanics, so its presence is interesting. Eight constants need to be eliminated: \( (c_{1},\overrightarrow{C_{1}}) \) and \( (c_{2},\overrightarrow{C}_{2}) \). Take the derivative of the spacetime position with respect to \( \tau \). This eliminates four constants, \( (c_{2},\overrightarrow{C}_{2}) \). The result is a 4-velocity: \begin{eqnarray} \frac{\partial t}{\partial \tau } & = & c_{1}e^{\frac{GM}{c^{2}\tau }}\nonumber \\ \frac{\partial \overrightarrow{R}}{\partial \tau } & = & \overrightarrow{C}_{1}e^{-\frac{GM}{c^{2}\tau }}.\label{solution_velocity} \end{eqnarray} In flat spacetime, \( U_{\mu }U^{\mu }=1 \), providing four more constraints. Spacetime is flat if \( M\rightarrow 0 \) or \( \tau \rightarrow \infty \), leading to \( e^{\pm \frac{GM}{c^{2}\tau }}\rightarrow 1 \): \begin{equation} \label{flat_constraint} (\frac{\partial t}{\partial \tau })^{2}-(\frac{\partial \overrightarrow{R}}{\partial \tau })\cdot (\frac{\partial \overrightarrow{R}}{\partial \tau })=c_{1}^{2}-\overrightarrow{C}_{1}\cdot \overrightarrow{C}_{1}=1. \end{equation} Solve for \( c_{1}^{2} \) and \( \overrightarrow{C}_{1}\cdot \overrightarrow{C}_{1} \): \begin{eqnarray} c_{1}^{2} & = & e^{-2\frac{GM}{c^{2}\tau }}(\frac{\partial t}{\partial \tau })^{2}\nonumber \\ \overrightarrow{C}_{1}\cdot \overrightarrow{C}_{1} & = & e^{2\frac{GM}{c^{2}\tau }}(\frac{\partial \overrightarrow{R}}{\partial \tau })\cdot (\frac{\partial \overrightarrow{R}}{\partial \tau }).\label{constants} \end{eqnarray} Substitute back into the flat spacetime constraint. Rearrange into a metric: \begin{equation} \label{new_metric} (\partial \tau )^{2}=e^{-2\frac{GM}{c^{2}\tau }}(\partial t)^{2}-e^{2\frac{GM}{c^{2}\tau }}(\partial \overrightarrow{R})^{2}. \end{equation} As expected, this becomes the Minkowski metric for flat spacetime if \( M\rightarrow 0 \) or \( \tau \rightarrow \infty \). For a weak field, write the Taylor series expansion in terms of the source mass over the interval to second-order in \( \frac{GM}{c^{2}\tau } \): \[ \partial \tau ^{2}=(1-2\frac{GM}{c^{2}\tau }+2(\frac{GM}{c^{2}\tau })^{2})\partial t^{2}-\] \begin{equation} \label{weak_field_metric} -(1+2(\frac{GM}{c^{2}\tau })+2(\frac{GM}{c^{2}\tau })^{2})\partial \overrightarrow{R}^{2}+O((\frac{GM}{c^{2}\tau })^{3}). \end{equation} Contrast this with the Schwarzschild solution in isotropic coordinates expanded to second order in \( \frac{GM}{c^{2}R} \)\cite[Eq. 31.22]{misner1970}: \[ \partial \tau ^{2}=(1-2\frac{GM}{c^{2}R}+2(\frac{GM}{c^{2}R})^{2})\partial t^{2}-\] \begin{equation} \label{schwarzschild_metric} -(1+2(\frac{GM}{c^{2}R})+2.5(\frac{GM}{c^{2}R})^{2})\partial \overrightarrow{R}^{2}+O((\frac{GM}{c^{2}R})^{3}). \end{equation} The magnitude of the lightlike interval \( \tau \) in Eq. \ref{weak_field_metric} is nearly identical to the radius \( R \) in the Schwarzschild metric, the difference being the geometric mass of the source included in the interval \( \tau \). The metric for the scalar potential will pass the same weak field tests of general relativity as the Schwarzschild metric to post-Newtonian accuracy, which does not use the second order spatial term.\cite{will1993} The difference in the higher order terms can be the basis of an experimental test to distinguish this proposal from general relativity. Since the effect is second order in the field term, such a test will challenge experimental techniques. The two metrics are numerically very similar for weak fields, but mathematically distinct. For example, the Schwarzschild metric is static, but the new metric contains a dependence on time, so is dynamic (but only locally, for small amounts of time). The Schwarzschild metric has a singularity at \( R=0 \). The metric for the scalar mode becomes undefined for lightlike intervals. This might pose less of a conceptual problem, since light has no rest mass, and the transverse mode describes the motion of massless particles. \section{A constant velocity profile solution} There are two problems with a classical Newtonian gravity explanation of the flat velocity profiles of thin spiral galaxies with a mass distribution that decays exponentially. \cite{freeman1970,kent1986,kent1987,vanalbada1985} First, the galaxies should have a Keplarian decline in the velocity profile with distance.\cite{toomre1963} Second, the a thin spiral galaxy is not stable a stable solution because a small disturbance should cause it to collapse.\cite{toomre1964} The work on dark matter is an attempt to remedy these problems. In the previous section, the system had a constant effective point-source mass with a velocity profile that decayed with distance. Here in an attempt to explain the spiral galaxies, the opposite situation is examined, where the velocity profile is a constant, but the mass distribution decays exponentially with distance. The force equation in this situation is: \begin{equation} \label{constant_v_force} U^{\mu }\frac{\partial m}{\partial \tau }=m\frac{\partial ^{\mu }A^{\nu }}{|A|}U_{\nu }. \end{equation} Gravity's effect is on the distribution of mass over spacetime where the velocity is constant. Make the same assumptions as used before. Presume a inverse interval squared potential. The interval \( \tau \) has nearly the same magnitude as the distance between the source and test masses, except that it includes the source mass expressed as a distance. Assuming the equivalence principle this time does not lead to the cancellation of the test mass, but instead allows the test mass to be the focus of the following differential equation: \begin{equation} \label{mass_distribution} (\gamma (\frac{\partial m}{\partial \tau }+\frac{GM}{c^{2}\tau ^{2}}m),\gamma \overrightarrow{\beta }(\frac{\partial m}{\partial \tau }-\frac{GM}{c^{2}\tau ^{2}}m))=(0,\overrightarrow{0}). \end{equation} Solve for the mass flow: \begin{equation} \label{mass_flow} (\gamma m,\gamma \overrightarrow{\beta }m)=(ce^{\frac{GM}{c^{2}\tau }},\overrightarrow{C}e^{-\frac{GM}{c^{2}\tau }}). \end{equation} The velocity is constant, so it is the test mass distribution that shows an exponential decay with respect to the interval, which is numerically almost the same as the radius. This is a stable solution. If the test mass keeps dropping of exponentially, the velocity profile will remain constant. Look at the problem in reverse. The distribution of mass has an exponential decay with distance from the center. It must solve a differential equation with the velocity constant over that region of spacetime like the one proposed. The exponential decay of the mass of a disk galaxy is only one solution to the gravitational force equation (Eq. \ref{4-force}). The behavior of larger systems, such as gravitational lensing caused by clusters, cannot be explained by the Newton's law.\cite{bergmann1990}\cite{grossman1989}\cite{tyson1990} It will remain to be seen if this proposal is sufficient to work on that scale. \section{Future directions} An algebraic path between a solution to the Maxwell equations in the Lorenz gauge and a metric gravitational theory has been shown. Like the early work in quantum mechanics, a collection of hunches is used to connect equations. One is left with the question of why this might work? Fortunately the answer is subtle enough that I did not have to mention my own area of study, four dimensional division algebras. The action of a gauge invariant theory cannot be inverted to generate the propagator needed for quantum mechanics.\cite{kaku1993} Fixing the gauge makes the action invertible. This may appear to be a technical feature, but the author believes this is vital. If the operation of multiplication surpasses what can be done with division, then Nature cannot harness the most robust mathematical structure, a topological algebraic field, the foundation for doing calculus. Nature does calculus in four dimensions, and it is this requirement that fixes the gauge. In the future, when we understand how to do calculus with four dimensional automorphic functions, we may have a deep appreciation of Nature's methods. For a spiral galaxy with an exponential mass distribution, dark matter is no longer needed to explain the flat velocity profile observed or the long term stability of such disks. Mass distributed over large distances of space has an effect on the mass distribution itself. This raises an interesting question: is there also an effect of mass distributed over large amounts of time? If the answer is yes, then this might solve two analogous riddles involving large time scales, flat velocity profiles and the stability of solutions. Classical big bang cosmology theory spans the largest time frame possible and faces two such issues. The horizon problem involves the extremely consistent velocity profile across parts of the Universe that are not casually linked.\cite[p. 815]{misner1970} The flatness problem indicates how unstable the classical big bang theory is, requiring exceptional fine tuning to avoid collapse.\cite{dicke1979} Considerable effort will be required to substantiate this tenuous hypothesis. Any insight into the origin of the unified engine driving the Universe of gravity and light is worthwhile. \bibliographystyle{plain} \bibliography{references} \vspace{0.3cm} \end{document} ########## references ########## @book{misner1970, author="Misner, C. W. and Thorne, K. S. and Wheeler, J. A.", title="Gravitation", publisher="W. H. Freeman and Company", place="New York", isbn=0716703440, year=1970} @article{kraichnan1955, author="Kraichnan, R. H.", title="Special-relativistic derivation of generally covariant gravitation theory", journal="Phys. Rev.", volume=55, pages="1118--1122", callnumber="QC.P579", year=1955} @book{will1993, author="Will, C. M.", title="Theory and experiment in gravitational physics: Revised edition", publisher="Cambridge University Press", isbn=0521439736, year=1993} @book{kaku1993, author="Kaku, M.", title="Quantum field theory: A modern introduction", publisher="Oxford University Press", place="New York, London", year=1993} @article{freeman1970, author="Freeman, K. C.", title="On the disks of spiral and SO galaxies", journal="Astrophys. J.", volume=160, pages="811--830", year=1970, callnumber="QB.A861", dougnumber="87.72.34.1", comment="exponential decay on the disk, indep of sphere"} @article{kent1986, author="Kent, S. M.", title="Dark matter in spiral galaxies. I. Galaxies with optical rotation curves", journal="Astron. J.", volume=91, number=6, pages="1301--1327", dougnumber="87.79.44.1", year=1986} @article{kent1987, author="Kent, S. M.", title="Dark matter in spiral galaxies. II. Galaxies with H1 rotation curves", journal="Astron. J.", volume=93, number=4, pages="816--832", year=1987, dougnumber="87.79.45.1", comment="With neutral H curves, all need dark matter"} @article{vanalbada1985, author="van Albada, T. S. and Bahcall, J. N. and Sanscisi, R.", title="Distribution of dark matter in the spiral galaxy NGC 3198", journal="Astrophys. J.", volume=295, number=2, pages="305-313", year=1985, callnumber="QB.A861", dougnumber="87.79.40.1", comment="Use hydrogen gas to see flat velocity curve way out there"} @article{grossman1989, author="Grossman, S. A. and Narayan, R.", title="Gravitationally lensed images in Abell 370", journal="Astrophys. J.", volume=344, pages="637-644", callnumber="QB.A861", year=1989} @article{bergmann1990, author="Bergmann, A. G. and Petrosian, V. and Lynds, R.", title="Gravitational lens images of arcs in clusters", journal="Astrophys. J.", volume=350, pages=23, callnumber="QB.A861", year=1990} @article{tyson1990, author="Tyson, J. A. and Valdes, F. and Wenk, R. A", title="Detection of systematic gravitational lens galaxy image alignments: Mapping dark matter in galaxy clusters", journal="Astrophys. J. Let.", volume=349, pages="L1", year=1990} @article{toomre1963, author="Toomre, A.", title="On the distribution of matter within highly flattened galaxies", journal="Astrophys. J.", volume=138, number=2, pages="385--392", year=1963, callnumber="QB.A861", dougnumber="", comment="uses elliptical integrals to go from light distribution to mass"} --87.79.51.1 @article{toomre1964, author="Toomre, A.", title="On the gravitational stability of a disk of stars", journal="Astrophys. J.", volume=139, pages=1217, callnumber="QB.A861", dougnumber="", year=1964} @article{guth1981, author="Guth, A. H.", title="Inflationary universe: A possible solution to the horizon and flatness problems", journal="Phys. Rev. D", volume=23, pages="347--356", callnumber="QC.P5814", year=1981} @book{dicke1979, author="Dicke,R. H. and Peebles, P. J. E.", title="General relativity: An Einstein centenary survey", publisher="Cambridge University Press", place="London", callnumber="QC173.6.G64", year=1979} @article{gupta1950, author="S. N. Gupta", title="Thoery of longitudinal photons in quantum electrodynamics", journal="Proc. Phys. Soc.", volume=63, pages="681--691", year=1950}
Resubmission request
Dear Dr Sweetser,
Thank you for submission.
But, I am on Windows computer and
many macros which you used cannot
be processed here. Please use 12pt.sty,
article.sty and delete other packages.
Please also include the bibliography
in the same file.
I am afraid that the same problems will appear
on referee's computers.
Sincerely,
Resubmission
Hello Prof. Dvoeglazov:
As requested, the header has been greatly simplified. The only extra
package required is latexsym needed for a d'Alembertian operator, which
is quiet standard.
The bibliography is included at the end.
The length of the paper is now 11 pages, although with my chosen font
it came out to 10. Hopefully we can consider this rounding error.
Sincerely,
\documentclass[12pt]{article}
\usepackage{latexsym}
\begin{document}
\title{There is no place like home: Looking for a metric equation for gravity
within the structure of the Maxwell equations}
\author{Douglas B. Sweetser}
\maketitle
1340 Commonwealth Ave. Apt. 7, Allston, MA 02134
\begin{abstract}
The Maxwell equations written in the Lorenz gauge are known, at least
mathematically, to have four modes of transmission: two transverse
modes for electrodynamics, a longitudinal, and a scalar mode. The
probabilities of the last two modes cancel each other out for photons
in a vacuum, but that does not have to be the case for a nonhomogeneous
equation. One scalar potential solution to the equations of motion
is found, the inverse of an interval between two events squared. The
force field created by the potential is constructed by comparison
with the classical Newtonian field. The Lagrangian \( L=-J^{\mu }A_{\mu }-\frac{1}{2}(\partial ^{\mu }A^{\nu })(\partial _{\mu }A_{\nu }) \)
can contribute to the scalar mode, but still forms the Maxwell equations
in the Lorenz gauge. A relativistic force equation is proposed, created
by the product of charge, normalized force field, and 4-velocity:
\( \frac{\partial mU^{\mu }}{\partial \tau }=kq\frac{\partial ^{\mu }A^{\nu }}{|A|}U_{\nu } \).
The solution to the force equation using the inverse square interval
potential is found. Eliminating the constants generates a metric equation,
\( (\partial \tau )^{2}=e^{-2\frac{GM}{c^{2}\tau }}(\partial t)^{2}-e^{2\frac{GM}{c^{2}\tau }}(\partial \overrightarrow{R})^{2} \),
where \( \tau \) is a lightlike interval with almost the same magnitude
as the radius \( R \) of separation between source and test masses.
For a weak gravitational field, the metric will pass the same tests
as the Schwarzschild metric of general relativity. The two metrics
differ for higher order terms, which makes the proposed metric distinct
and testable experimentally. A constant-velocity solution exists for
the gravitational force equation for a system with an exponentially-decaying
mass distribution. The dark matter hypothesis is not needed to explain
the constant-velocity profiles seen for some galaxies. The proposal
may also have implications for classical big bang theory.
\end{abstract}
\section{An opportunity for gravity}
The Maxwell equations can be quantized in a manifestly covariant form
by fixing the gauge.\cite{gupta1950} The starting point is the 4-potential
\( A^{\mu } \). There are four modes of transmission for photons
corresponding to the four degrees of freedom: two transverse, one
scalar, and one longitudinal. Gupta calculated that for photons in
a vacuum, the probability of the scalar mode cancels that of the longitudinal
mode, so both are virtual. He notes that this does not alway have
to be the case for the nonhomogeneous Maxwell equations, which is
the focus of this work.
My hypothesis is that a dominant scalar mode for the Maxwell equations
in the Lorenz gauge is gravity. The hypothesis makes several predictions
even at this preliminary stage. First, the math of gravity and electromagnetism
should be similar but not identical. The inverse square form of Newton's
law of gravity was a direct inspiration for Coulomb's law. Gravity
should be more symmetric than electromagnetism because the mode is
scalar, instead of transverse. The second rank field strength tensor
in general relativity is symmetric while the analogous tensor for
the electromagnetic field is antisymmetric. Since the mode of gravity
is orthogonal to electromagnetism, the charges can be likewise, so
there will be no simple relationship between gravitational charge
(mass) and electric charge. Gravitational waves in general relativity
are transverse, so this proposal is distinct from general relativity.
Nature exploits all the math available, so it is unreasonable to suppose
that the scalar mode is never used for anything. Whatever phenomenon
exploits the scalar mode must be similar, but just as important as
electromagnetism. Gravity is a natural candidate.
An algebraic road will be constructed starting from a solution to
the Maxwell equations in the Lorenz gauge to a curved metric. Many
of the steps will be justified by the need to be consistent with Newton's
law of gravity in the classical limit. The reward of this work is
a metric which is similar enough to the Schwarzschild metric of general
relativity to agree with all the experimental results to post-Newtonian
accuracy, yet differs for higher order terms. Thus the proposal can
be confirmed or refuted by more precise tests of the metric. The second
major prediction concerns the velocity profile of spiral galaxies.
For a mass distribution that decays exponentially, the equations of
motion for the scalar mode predict a stable and flat velocity profile
with increasing radius. This eliminates the need for the dark matter
hypothesis.
\section{A gravitational field inside Maxwell}
Newton's classical gravitational law arises from a scalar potential.
Here is the scalar field equation:
\begin{equation}
\label{poisson}
\nabla ^{2}\phi =4\pi G\rho .
\end{equation}
For the case of a vacuum, when \( \rho =0 \), this is known as the
Laplace equation. For a spherically symmetric source, one solution
is:
\begin{equation}
\label{potential}
\phi =-\frac{GM}{\sqrt{x^{2}+y^{2}+z^{2}}}.
\end{equation}
The problem with the field equation is that the Laplace operator does
not have a time differential. Any change in in the mass density propagates
at infinite speed, in conflict with special relativity.\cite[Chapter 7]{misner1970}
One way to derive the field equations of general relativity involves
making Newton's law of gravity consistent with the finite speed of
light.\cite{kraichnan1955}
A way to repair the field equations is to use the D'Alembertian operator,
which is four dimensional. That expression is identical to the \( A^{0} \)
component of the Maxwell equations in the Lorenz gauge:
\begin{equation}
\label{max_in_lorena_gauge}
\Box ^{2}A^{\mu }=4\pi kJ^{\mu }.
\end{equation}
If one is studying scalar (or possibly longitudinal) modes, \( J^{\mu } \)
is the mass density. If one is working with transverse modes, \( J^{\mu } \)
is the electric charge density. Since the modes are orthogonal, the
sources can be also.
To be consistent with the classic scalar potential yet still be relativistic,
the potential must have \( x^{2} \), \( y^{2} \), \( z^{2} \),
and \( t^{2} \). This suggests a particular solution to the field
equations (Eq. \ref{max_in_lorena_gauge}):
\begin{equation}
\label{1/taupotential}
A^{\mu }=(\frac{1}{c^{2}t^{2}-x^{2}-y^{2}-z^{2}},0,0,0).
\end{equation}
This potential is interesting for several reasons. It is the inverse
of the Lorentz-invariant interval squared. Like mass, the 4-potential
will not be altered by a change in an inertial reference frame. The
interval between any two events will contribute to the potential.
General relativity applies to any form of energy, including gravitational
field energy. A potential that embraces every interval may have a
broad enough scope to do the work of gravity.
The potential also has serious problems. Classical gravity depends
on an inverse square force field, not an inverse square potential.
Taking the derivative of the potential puts a fourth power of the interval
in the denominator. At this point, I could stop and say that this
potential has nothing to do with gravity because it has the wrong
dependence on distance. An alternative is to look for an algebraic
way to repair the problem. This is the type of approach used by the
early workers in quantum mechanics like de Broglie, and will be adopted
here. The equations of motion (Eq. \ref{max_in_lorena_gauge}) can
be normalized to the magnitude of the 4-potential:
\begin{equation}
\label{normalized_max}
\frac{\Box ^{2}A^{\mu }}{|A|}=4\pi kJ^{\mu }.
\end{equation}
Since the magnitude of the potential is the inverse interval squared,
the resulting equation has only an interval squared in the denominator.
An interval is not necessarily the same as the distance R between
the source and test mass used in the classical theory. However, I
can impose a selection rule that in the classical limit, the only
events that contribute to the potential are those that are timelike
separated between the source and the test masses. It takes a timelike
interval to know that the source is a distance R away. Action-at-a-distance
respects the speed of light as it must.
\section{Search for the source mass}
Where is the source mass in the potential? All that has been discussed
so far is an interval, a distance, nothing about mass. An idea from
general relativity will be borrowed, that mass can be treated geometrically
if multiplied by the constants \( \frac{G}{c^{2}} \). The distance
between the Earth and the Sun is approximately \( 1.5x10^{11}m \),
while the Sun's mass expressed in units of distance, \( \frac{G\mathrm{M}_{Sun}}{c^{2}} \),
is \( 1.5x10^{3}m \), eight orders of magnitude smaller. The overall
length of the interval will not be changed noticeably if the spatial
separation and the Sun's mass expressed as a distance are summed.
However, the force field is the derivative of the potential, and any
change in position in spacetime will have a far greater effect proportionally
on the smaller geometric mass than the spatial separation. Make the
following change of variables:
\begin{eqnarray}
t & \rightarrow & t'=A+\frac{GM}{2c^{2}A}t\nonumber \\
\overrightarrow{R} & \rightarrow & \overrightarrow{R}'=\overrightarrow{B}+\frac{GM}{2c^{2}|\overrightarrow{B}|}\overrightarrow{R},\label{small_change}
\end{eqnarray}
where \( A \) and \( \overrightarrow{B} \) are locally constants
such that \( \tau ^{2}\cong A^{2}-\overrightarrow{B}^{2} \). The
change of variables is valid locally, but not globally, since it breaks
down for arbitrarily long time or distance away. General relativity
is also valid locally and not globally. The derivative of the normalized
interval squared is approximately:
\begin{eqnarray}
\frac{1}{|\frac{1}{\tau ^{2}}|}\frac{\partial \frac{1}{\tau ^{2}}}{\partial t} & \cong & -\frac{GM}{c^{2}\tau ^{2}}\nonumber \\
\frac{1}{|\frac{1}{\tau ^{2}}|}\overrightarrow{\nabla }\frac{1}{\tau ^{2}} & \cong & \frac{GM}{c^{2}\tau ^{2}}\widehat{R}.\label{derpotential}
\end{eqnarray}
This should look familiar, remembering that the magnitude of \( \tau ^{2} \)
is the same as \( R^{2} \), differing only by the geometric mass
of the source.
\section{A Lagrangian for four modes}
Gupta wanted to quantize the Maxwell equations using a form that was
manifestly covariant in its explicit treatment of time and space.
He fixed the gauge with this Lagrangian:
\begin{equation}
\label{gupta_Lagrangian}
L=-J^{\mu }A_{\mu }-\frac{1}{2}(\partial ^{\mu }A_{\mu })^{2}-\frac{1}{4}(\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu })(\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }).
\end{equation}
The equations of motion for this Lagrangian are the Maxwell equations
in the Lorenz gauge (Eq. \ref{max_in_lorena_gauge}). The problem
with the Lagrangian is that the field strength tensor is antisymmetric.
Due to the zeros along the diagonal, it cannot contribute directly
to a scalar mode. What is needed is a Lagrangian that could contribute
directly to the scalar mode but still have the same equation of motion.
Here is such a Lagrangian:
\begin{equation}
\label{4modelagrangian}
L=-J^{\mu }A_{\mu }-\frac{1}{2}(\partial ^{\mu }A^{\nu })(\partial _{\mu }A_{\nu }).
\end{equation}
This is not as miraculous as it might first appear. It is the first
of four terms generated in the contraction of the electromagnetic
field strength tensor. In essence, I have chosen not to discard information,
which is what happens in making the field strength tensor antisymmetric.
The one remaining modification is to normalize both the Lagrangian
and equations of motion to the size of the potential.
\section{From a 4-force to a metric}
A relativistic 4-force is the change in momentum with respect to the
interval. The covariant force law is similar in form to the one for
electromagnetism except that the second rank tensor is asymmetric
and normalized:
\begin{equation}
\label{4-force}
F=\frac{\partial p}{\partial \tau }=m\frac{\partial U^{\mu }}{\partial \tau }+U^{\mu }\frac{\partial m}{\partial \tau }=kq\frac{\partial ^{\mu }A^{\nu }}{|A|}U_{\nu }.
\end{equation}
In the first application of the force law, assume the derivative of
the mass with respect to the interval is zero. For the scalar mode,
assume the charge \( q \) is the gravitational test mass. Experiments
have demonstrated that gravitational and inertial masses are equal.\cite{will1993}
The inverse interval squared potential leads to the following equation
of motion:
\begin{equation}
\label{classical_force_law}
(\frac{\partial ^{2}t}{\partial \tau ^{2}}+\frac{GM}{c^{2}\tau ^{2}}\frac{\partial t}{\partial \tau },\frac{\partial ^{2}\overrightarrow{R}}{\partial \tau ^{2}}-\frac{GM}{c^{2}\tau ^{2}}\frac{\partial \overrightarrow{R}}{\partial \tau })=(0,\overrightarrow{0}).
\end{equation}
Solve this second-order differential equation for the spacetime position:
\begin{eqnarray}
t & = & c_{1}(\tau e^{\frac{GM}{c^{2}\tau }}-\frac{GM}{c^{2}}Ei(\frac{GM}{c^{2}\tau }))+c_{2}\nonumber \\
\overrightarrow{R} & = & \overrightarrow{C}_{1}(\tau e^{-\frac{GM}{c^{2}\tau }}+\frac{GM}{c^{2}}Ei(-\frac{GM}{c^{2}\tau }))+\overrightarrow{C}_{2},\label{solution}
\end{eqnarray}
where Ei is the exponential integral, \( Ei(t)=\int ^{t}_{-\infty }\frac{e^{t}}{t}dt \).
The exponential integral plays a role in quantum mechanics, so its
presence is interesting.
Eight constants need to be eliminated: \( (c_{1},\overrightarrow{C_{1}}) \)
and \( (c_{2},\overrightarrow{C}_{2}) \). Take the derivative of
the spacetime position with respect to \( \tau \). This eliminates
four constants, \( (c_{2},\overrightarrow{C}_{2}) \). The result
is a 4-velocity:
\begin{eqnarray}
\frac{\partial t}{\partial \tau } & = & c_{1}e^{\frac{GM}{c^{2}\tau }}\nonumber \\
\frac{\partial \overrightarrow{R}}{\partial \tau } & = & \overrightarrow{C}_{1}e^{-\frac{GM}{c^{2}\tau }}.\label{solution_velocity}
\end{eqnarray}
In flat spacetime, \( U_{\mu }U^{\mu }=1 \), providing four more
constraints. Spacetime is flat if \( M\rightarrow 0 \) or \( \tau \rightarrow \infty \),
leading to \( e^{\pm \frac{GM}{c^{2}\tau }}\rightarrow 1 \):
\begin{equation}
\label{flat_constraint}
(\frac{\partial t}{\partial \tau })^{2}-(\frac{\partial \overrightarrow{R}}{\partial \tau })\cdot (\frac{\partial \overrightarrow{R}}{\partial \tau })=c_{1}^{2}-\overrightarrow{C}_{1}\cdot \overrightarrow{C}_{1}=1.
\end{equation}
Solve for \( c_{1}^{2} \) and \( \overrightarrow{C}_{1}\cdot \overrightarrow{C}_{1} \):
\begin{eqnarray}
c_{1}^{2} & = & e^{-2\frac{GM}{c^{2}\tau }}(\frac{\partial t}{\partial \tau })^{2}\nonumber \\
\overrightarrow{C}_{1}\cdot \overrightarrow{C}_{1} & = & e^{2\frac{GM}{c^{2}\tau }}(\frac{\partial \overrightarrow{R}}{\partial \tau })\cdot (\frac{\partial \overrightarrow{R}}{\partial \tau }).\label{constants}
\end{eqnarray}
Substitute back into the flat spacetime constraint. Rearrange into
a metric:
\begin{equation}
\label{new_metric}
(\partial \tau )^{2}=e^{-2\frac{GM}{c^{2}\tau }}(\partial t)^{2}-e^{2\frac{GM}{c^{2}\tau }}(\partial \overrightarrow{R})^{2}.
\end{equation}
As expected, this becomes the Minkowski metric for flat spacetime
if \( M\rightarrow 0 \) or \( \tau \rightarrow \infty \). For a
weak field, write the Taylor series expansion in terms of the source
mass over the interval to second-order in \( \frac{GM}{c^{2}\tau } \):
\[
\partial \tau ^{2}=(1-2\frac{GM}{c^{2}\tau }+2(\frac{GM}{c^{2}\tau })^{2})\partial t^{2}-\]
\begin{equation}
\label{weak_field_metric}
-(1+2(\frac{GM}{c^{2}\tau })+2(\frac{GM}{c^{2}\tau })^{2})\partial \overrightarrow{R}^{2}+O((\frac{GM}{c^{2}\tau })^{3}).
\end{equation}
Contrast this with the Schwarzschild solution in isotropic coordinates
expanded to second order in \( \frac{GM}{c^{2}R} \)\cite[Eq. 31.22]{misner1970}:
\[
\partial \tau ^{2}=(1-2\frac{GM}{c^{2}R}+2(\frac{GM}{c^{2}R})^{2})\partial t^{2}-\]
\begin{equation}
\label{schwarzschild_metric}
-(1+2(\frac{GM}{c^{2}R})+2.5(\frac{GM}{c^{2}R})^{2})\partial \overrightarrow{R}^{2}+O((\frac{GM}{c^{2}R})^{3}).
\end{equation}
The magnitude of the lightlike interval \( \tau \) in Eq. \ref{weak_field_metric}
is nearly identical to the radius \( R \) in the Schwarzschild metric,
the difference being the geometric mass of the source included in
the interval \( \tau \). The metric for the scalar potential will
pass the same weak field tests of general relativity as the Schwarzschild
metric to post-Newtonian accuracy, which does not use the second order
spatial term.\cite{will1993} The difference in the higher order terms
can be the basis of an experimental test to distinguish this proposal
from general relativity. Since the effect is second order in the field
term, such a test will challenge experimental techniques.
The two metrics are numerically very similar for weak fields, but
mathematically distinct. For example, the Schwarzschild metric is
static, but the new metric contains a dependence on time, so is dynamic
(but only locally, for small amounts of time). The Schwarzschild metric
has a singularity at \( R=0 \). The metric for the scalar mode becomes
undefined for lightlike intervals. This might pose less of a conceptual
problem, since light has no rest mass, and the transverse mode describes
the motion of massless particles.
\section{A constant velocity profile solution}
There are two problems with a classical Newtonian gravity explanation
of the flat velocity profiles of thin spiral galaxies with a mass
distribution that decays exponentially. \cite{freeman1970,kent1986,kent1987,vanalbada1985}
First, the galaxies should have a Keplarian decline in the velocity
profile with distance.\cite{toomre1963} Second, a thin spiral
galaxy is not stable a stable solution because a small disturbance
should cause it to collapse.\cite{toomre1964} The work on dark matter
is an attempt to remedy these problems.
In the previous section, the system had a constant effective point-source
mass with a velocity profile that decayed with distance. Here in an
attempt to explain the spiral galaxies, the opposite situation is
examined, where the velocity profile is a constant, but the mass distribution
decays exponentially with distance. The force equation in this situation
is:
\begin{equation}
\label{constant_v_force}
U^{\mu }\frac{\partial m}{\partial \tau }=m\frac{\partial ^{\mu }A^{\nu }}{|A|}U_{\nu }.
\end{equation}
Gravity's effect is on the distribution of mass over spacetime where
the velocity is constant. Make the same assumptions as used before.
Presume an inverse interval squared potential. The interval \( \tau \)
has nearly the same magnitude as the distance between the source and
test masses, except that it includes the source mass expressed as
a distance. Assuming the equivalence principle this time does not
lead to the cancellation of the test mass, but instead allows the
test mass to be the focus of the following differential equation:
\begin{equation}
\label{mass_distribution}
(\gamma (\frac{\partial m}{\partial \tau }+\frac{GM}{c^{2}\tau ^{2}}m),\gamma \overrightarrow{\beta }(\frac{\partial m}{\partial \tau }-\frac{GM}{c^{2}\tau ^{2}}m))=(0,\overrightarrow{0}).
\end{equation}
Solve for the mass flow:
\begin{equation}
\label{mass_flow}
(\gamma m,\gamma \overrightarrow{\beta }m)=(ce^{\frac{GM}{c^{2}\tau }},\overrightarrow{C}e^{-\frac{GM}{c^{2}\tau }}).
\end{equation}
The velocity is constant, so it is the test mass distribution that
shows an exponential decay with respect to the interval, which is
numerically almost the same as the radius. This is a stable solution.
If the test mass keeps dropping of exponentially, the velocity profile
will remain constant.
Look at the problem in reverse. The distribution of mass has an exponential
decay with distance from the center. It must solve a differential
equation with the velocity constant over that region of spacetime
like the one proposed.
The exponential decay of the mass of a disk galaxy is only one solution
to the gravitational force equation (Eq. \ref{4-force}). The behavior
of larger systems, such as gravitational lensing caused by clusters,
cannot be explained by the Newton's law.\cite{bergmann1990}\cite{grossman1989}\cite{tyson1990}
It will remain to be seen if this proposal is sufficient to work on
that scale.
\section{Future directions}
An algebraic path between a solution to the Maxwell equations in the
Lorenz gauge and a metric gravitational theory has been shown. Like
the early work in quantum mechanics, a collection of hunches is used
to connect equations. One is left with the question of why this might
work? Fortunately the answer is subtle enough that I did not have
to mention my own area of study, four dimensional division algebras.
The action of a gauge invariant theory cannot be inverted to generate
the propagator needed for quantum mechanics.\cite{kaku1993} Fixing
the gauge makes the action invertible. This may appear to be a technical
feature, but the author believes this is vital. If the operation of
multiplication surpasses what can be done with division, then Nature
cannot harness the most robust mathematical structure, a topological
algebraic field, the foundation for doing calculus. Nature does calculus
in four dimensions, and it is this requirement that fixes the gauge.
In the future, when we understand how to do calculus with four dimensional
automorphic functions, we may have a deep appreciation of Nature's
methods.
For a spiral galaxy with an exponential mass distribution, dark matter
is no longer needed to explain the flat velocity profile observed
or the long term stability of such disks. Mass distributed over large
distances of space has an effect on the mass distribution itself.
This raises an interesting question: is there also an effect of mass
distributed over large amounts of time? If the answer is yes, then
this might solve two analogous riddles involving large time scales,
flat velocity profiles and the stability of solutions. Classical big
bang cosmology theory spans the largest time frame possible and faces
two such issues. The horizon problem involves the extremely consistent
velocity profile across parts of the Universe that are not casually
linked.\cite[p. 815]{misner1970} The flatness problem indicates how
unstable the classical big bang theory is, requiring exceptional fine
tuning to avoid collapse.\cite{dicke1979} Considerable effort will
be required to substantiate this tenuous hypothesis. Any insight into
the origin of the unified engine driving the Universe of gravity and
light is worthwhile.
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{bergmann1990}
A.~G. Bergmann, V.~Petrosian, and R.~Lynds.
\newblock Gravitational lens images of arcs in clusters.
\newblock {\em Astrophys. J.}, 350:23, 1990.
\bibitem{dicke1979}
R.~H. Dicke and P.~J.~E. Peebles.
\newblock {\em General relativity: An Einstein centenary survey}.
\newblock Cambridge University Press, 1979.
\bibitem{freeman1970}
K.~C. Freeman.
\newblock On the disks of spiral and so galaxies.
\newblock {\em Astrophys. J.}, 160:811--830, 1970.
\bibitem{grossman1989}
S.~A. Grossman and R.~Narayan.
\newblock Gravitationally lensed images in abell 370.
\newblock {\em Astrophys. J.}, 344:637--644, 1989.
\bibitem{gupta1950}
S.~N. Gupta.
\newblock Theory of longitudinal photons in quantum electrodynamics.
\newblock {\em Proc. Phys. Soc.}, 63:681--691, 1950.
\bibitem{kaku1993}
M.~Kaku.
\newblock {\em Quantum field theory: A modern introduction}.
\newblock Oxford University Press, 1993.
\bibitem{kent1986}
S.~M. Kent.
\newblock Dark matter in spiral galaxies. i. galaxies with optical rotation
curves.
\newblock {\em Astron. J.}, 91(6):1301--1327, 1986.
\bibitem{kent1987}
S.~M. Kent.
\newblock Dark matter in spiral galaxies. ii. galaxies with h1 rotation curves.
\newblock {\em Astron. J.}, 93(4):816--832, 1987.
\bibitem{kraichnan1955}
R.~H. Kraichnan.
\newblock Special-relativistic derivation of generally covariant gravitation
theory.
\newblock {\em Phys. Rev.}, 55:1118--1122, 1955.
\bibitem{misner1970}
C.~W. Misner, K.~S. Thorne, and J.~A. Wheeler.
\newblock {\em Gravitation}.
\newblock W. H. Freeman and Company, 1970.
\bibitem{toomre1963}
A.~Toomre.
\newblock On the distribution of matter within highly flattened galaxies.
\newblock {\em Astrophys. J.}, 138(2):385--392, 1963.
\bibitem{toomre1964}
A.~Toomre.
\newblock On the gravitational stability of a disk of stars.
\newblock {\em Astrophys. J.}, 139:1217, 1964.
\bibitem{tyson1990}
J.~A. Tyson, F.~Valdes, and R.~A Wenk.
\newblock Detection of systematic gravitational lens galaxy image alignments:
Mapping dark matter in galaxy clusters.
\newblock {\em Astrophys. J. Let.}, 349:L1, 1990.
\bibitem{vanalbada1985}
T.~S. van Albada, J.~N. Bahcall, and R.~Sanscisi.
\newblock Distribution of dark matter in the spiral galaxy ngc 3198.
\newblock {\em Astrophys. J.}, 295(2):305--313, 1985.
\bibitem{will1993}
C.~M. Will.
\newblock {\em Theory and experiment in gravitational physics: Revised
edition}.
\newblock Cambridge University Press, 1993.
\end{thebibliography}
\vspace{0.3cm}
\end{document}
Request for reply
PS.I need your answers to referees.
Reply question
Hello Valeri:
I have two questions. First, should I reply with two documents, one
being a summary of my reply to their specific concerns, and the second
one being the revised paper itself? Second, what is the usual
reasonable time frame for the reply, a week?
Thanks,
Reply question answer
Dear Dr Sweetser,
Thank you for inquiry.
Doug B Sweetser wrote:
> Hello Valeri:
No, revisions of the paper text can be done only AFTER
the editor request; usually, after the editorial decision has
been sent to the author.
> Second, what is the usual
In your case, I believe, immediately. Moreover,
the first RR has been sent to you long ago.
Yours Sincerely,
Editor's comment
Dear Dr Sweetser,
I read your paper myself.
And my objection is the following:
you assume that (p.6) "for the scalar mode
the charge q is the gravitational test mass".
I believe,one should give some basis to this assumption,
because the electric charge may have two sign
(and the force can be attractive or repulsive).
For the gravity we do NOT know (yet?)
the repulsive force of the leading order (unless
higher orders have been taken into account,
but this generates other problems).
Please excuse me if I misunderstood your postulate.
Please answer.
Yours Sincerely,
Reply to editor
Hello Valeri:
My thoughts on this topic have evolved since I submitted this work,
due to feedback from the reviewers and discussions with a colleague.
Please allow me to provide an explanation so I can properly address
your question.
Based on worked done with 4-dimensional division algebras, I had come
to the conclusion that the typical analysis of 4-dimensional waves
was incomplete. Wanting to connect a mathematical observation to physics,
I cited Gupta's work with quantizing the electromagnetic field since
it dealt directly with the topic (I omitted Bleuler only due to my
inability to read German).
If I were to rewrite the paper today, I would delete the first paragraph
that refers to quantum mechanics. That would avoid the criticisms
of one of the reviewers. It would create a new problem for an entirely
classical motivation for the work. This is were I have made recent
progress.
Start with a 4-dimensional wave equation. We know that if the Lorenz
gauge is chosen, then the the result is the Maxwell equations, which
completely describe the behavior of the electromagnetic field. Electromagnetic
waves are composed of two transverse fields, so that two degrees of
freedom of the 4-potentially are accounted for. The only way to get
more information is to relax constraints. There is only one, the choice
of the Lorenz gauge. The question is, starting from a 4-dimensional
wave equation, can the Maxwell equations be generated along with a
set of equations for gravity with their own independent source? The
difference in sources is required because if the sources were directly
connected, we would have seen it by now in electrodynamics.
Start from a scalar wave equation, and try to recreate Gauss' equation
without assuming the Lorenz gauge:
The time derivative of the divergence of the 3-vector potential A
was added to the scalar wave equation. A small rearrangement creates
Gauss' law. There is also an equation for a field g. When written
in terms of potentials, the fields g, E and B compose the unified
asymmetric second rank field strength tensor. One might think that
there is no way a simple time derivative of the field g can be connected
to how we know gravity behaves. One cannot pass judgment until solutions
to the wave equation are found and studied, which is the bulk of my
paper.
Repeat the exercise for the 3-vector wave equation, trying to recreate
Ampere's law without assuming the Lorenz gauge:
The classical unified field equations are invariant under a gauge
transformation.
Now I can address your question. Here is the unified force equation:
Write out the force involving the electric field only:
What happens to the sign of the electric charge q under time or space
reversal? Nothing, because charge is a Lorentz invariant quantity.
It is completely uneffected. However, the electric field will change
sign under time or space reversal:
Repeat the same exercise for the gravitational force equation:
In the force laws for electricity and gravity, there is no way to
change the signs of the charge. With the electromagnetic force, the
antisymmetric part of the field strength tensor can flip signs under
a time or space inversion. That is not the case for the gravitation
force. It is the symmetry properties of the field strength tensor
which grant electromagnetism two signs for its charge, while gravity
only has one.
Thanks for your question. It was a delight to think about this weekend.
Sincerely,
Douglas Sweetser
Official rejection
I regret to inform you that the Paper cannot be published in this
issue of the Journal. Of course, you are now free to submit a revised
version to other Journal (including those where I am an editor).
I should like to take this opportunity to thank you for your
interest in ``Annales de Fondation Louis de Broglie".
Yours sincerely,
Offer for non-peer review publication
PS. While I informed you that this version of your paper
does NOT satisfy our criteria for the AFDB-special-issue project,
I can suggest to publish it as a regular paper of the electronic Journal
"Apeiron" http://redshift.vif.com (I am also an editor therein), due to
it suits more to its goals rather than other journals. This will be without
any further referee process. Just add the explanation about parity
on the page 6. But, it is necessary to convert it in the Apeiron MS Word
template,which can be found on the WEB site.
If you still prefer to develop this idea extensively and precisely,
you are welcomed to submit it later to Hadronic Journal (where I am
also an editor), but in this case it will be under review again by a
referee and an editor. If you would prefer to submit essentially
revised and enlarged version elsewhere, you may indicate me as a
referee. But, again, I consider that much work should be done on these
matters in order the paper to be suitable.
Yours,
Thanks for the offer
Hello Valeri:
The peer-review process did what it is designed to do: gave me a clear
direction for further work. Out will go any reference to quantum
mechanics, since all the techniques are classical. I also need a
clearer statement of my hypothesis, which involves a complete
characterization of 4D wave equations. That way I can say, this is my
hypothesis, not an arbitrary assumption, and these are the consequences
of that hypothesis. I don't mind if that involves much work :-)
The opening moves of a chess game are never novel. The pawns and the
knights must get out into the center. There are combinations
thousands have played. Coulomb himself probably spent a good deal of
time trying to unify Newton's law of gravity with his own law of
electrostatics. If you have a favorite source citation on classical
unification attempts, or know that one will appear in special issue of
AFDB, I would appreciate an email about it. It would be good to
clearly mark which of my moves is unique.
Thanks,
Home
Page | Quaternion Physics
|
Pop
Science
2001, doug <sweetser@alum.mit.edu>
All rights
reserved
worldwide
Return-Path:
Received: from ahobon.reduaz.mx (ahobon.reduaz.mx [148.217.51.3])
by TheWorld.com (8.9.3/8.9.3) with ESMTP id QAA24034
for
Received: from ahobon.reduaz.mx ([148.217.51.54])
by ahobon.reduaz.mx (8.9.3/8.9.3) with ESMTP id OAA26757
for
Message-ID: <3BBA2699.3D7CE0E0@ahobon.reduaz.mx>
Date: Tue, 02 Oct 2001 15:42:03 -0500
From: Valeri Dvoeglazov
X-Mailer: Mozilla 4.61 [en] (Win95; I)
X-Accept-Language: en,ru
MIME-Version: 1.0
To: sweetser@alum.mit.edu
Subject: Re: A submission to "Contemporary electrodynamics"
References: <200110010245.WAA07374@world.std.com>
Content-Type: text/plain; charset=us-ascii
Content-Transfer-Encoding: 7bit
Valeri Dvoeglazov
Guest Editor
To: Valeri Dvoeglazov
Reply-To: sweetser@alum.mit.edu
Subject: Simplifications for a submission to "Contemporary electrodynamics"
In-reply-to: Your message of "Tue, 02 Oct 2001 15:42:03 EDT."<3BBA2699.3D7CE0E0@ahobon.reduaz.mx>
Date: Tue, 02 Oct 2001 19:17:45 -0400
From: Doug B Sweetser
doug sweetser
Return-Path:
Received: from ahobon.reduaz.mx (ahobon.reduaz.mx [148.217.51.3])
by TheWorld.com (8.9.3/8.9.3) with ESMTP id RAA14479
for
Received: from ahobon.reduaz.mx ([148.217.51.54])
by ahobon.reduaz.mx (8.9.3/8.9.3) with ESMTP id PAA10594
for
Message-ID: <3BD48578.29238FA1@ahobon.reduaz.mx>
Date: Mon, 22 Oct 2001 15:45:44 -0500
From: Valeri Dvoeglazov
X-Mailer: Mozilla 4.61 [en] (Win95; I)
X-Accept-Language: en,ru
MIME-Version: 1.0
To: sweetser@alum.mit.edu
Subject: PS.
References: <200110022317.TAA29451@world.std.com>
Content-Type: text/plain; charset=us-ascii
Content-Transfer-Encoding: 7bit
VVD
To: Valeri Dvoeglazov
Reply-To: sweetser@alum.mit.edu
Subject: Re: PS.
In-reply-to: Your message of "Mon, 22 Oct 2001 15:45:44 EDT."<3BD48578.29238FA1@ahobon.reduaz.mx>
Date: Mon, 22 Oct 2001 22:34:10 -0400
From: Doug B Sweetser
Doug Sweetser
Return-Path:
Received: from ahobon.reduaz.mx (ahobon.reduaz.mx [148.217.51.3])
by TheWorld.com (8.9.3/8.9.3) with ESMTP id MAA14118
for
Received: from ahobon.reduaz.mx ([148.217.51.54])
by ahobon.reduaz.mx (8.9.3/8.9.3) with ESMTP id KAA12379
for
Message-ID: <3BD5909B.5211865F@ahobon.reduaz.mx>
Date: Tue, 23 Oct 2001 10:45:31 -0500
From: Valeri Dvoeglazov
X-Mailer: Mozilla 4.61 [en] (Win95; I)
X-Accept-Language: en,ru
MIME-Version: 1.0
To: sweetser@alum.mit.edu
Subject: Re: PS.
References: <200110230232.WAA29239@world.std.com>
Content-Type: text/plain; charset=koi8-r
Content-Transfer-Encoding: 7bit
>
> I have two questions. First, should I reply with two documents, one
> being a summary of my reply to their specific concerns, and the second
> one being the revised paper itself?
> reasonable time frame for the reply, a week?
>
>
> Thanks,
> Doug Sweetser
Valeri Dvoeglazov
Return-Path:
Received: from ahobon.reduaz.mx (ahobon.reduaz.mx [148.217.51.3])
by TheWorld.com (8.9.3/8.9.3) with ESMTP id OAA25656
for
Received: from ahobon.reduaz.mx ([148.217.51.54])
by ahobon.reduaz.mx (8.9.3/8.9.3) with ESMTP id MAA19824
for
Message-ID: <3BD99B50.29FDE3E4@ahobon.reduaz.mx>
Date: Fri, 26 Oct 2001 12:20:17 -0500
From: Valeri Dvoeglazov
X-Mailer: Mozilla 4.61 [en] (Win95; I)
X-Accept-Language: en,ru
MIME-Version: 1.0
To: sweetser@alum.mit.edu
Subject: my comments
References: <200110241703.NAA15118@world.std.com>
Content-Type: text/plain; charset=us-ascii
Content-Transfer-Encoding: 7bit
Valeri Dvoeglazov
To: Valeri Dvoeglazov
Reply-To: sweetser@alum.mit.edu
Subject: Re: my comments, a reply
In-reply-to: Your message of "Fri, 26 Oct 2001 12:20:17 EDT."<3BD99B50.29FDE3E4@ahobon.reduaz.mx>
Date: Sun, 28 Oct 2001 21:18:24 -0500
From: Doug B Sweetser 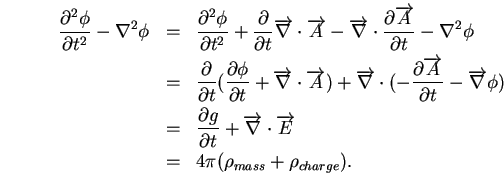
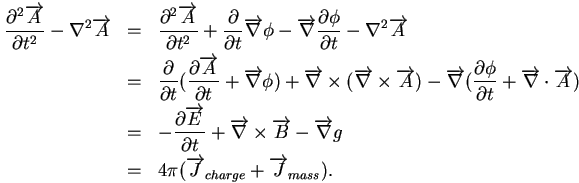

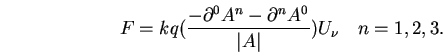
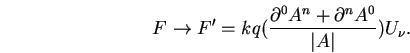
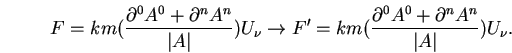
Return-Path:
Received: from cantera.reduaz.mx (cantera.reduaz.mx [148.217.2.30])
by TheWorld.com (8.9.3/8.9.3) with ESMTP id OAA21391
for
Received: from ahobon.reduaz.mx (unknown [148.217.51.54])
by cantera.reduaz.mx (Postfix) with ESMTP
id 6329D177E8; Mon, 29 Oct 2001 13:27:17 -0600 (CST)
Message-ID: <3BDDB1E9.9B1C6A8D@ahobon.reduaz.mx>
Date: Mon, 29 Oct 2001 13:45:46 -0600
From: Valeri Dvoeglazov
X-Mailer: Mozilla 4.61 [en] (Win95; I)
X-Accept-Language: en,ru
MIME-Version: 1.0
To: "sweetser@alum.mit.edu"
Subject: editorial decision AFDB/DVO/30
Content-Type: text/plain; charset=us-ascii
Content-Transfer-Encoding: 7bit
I am afraid that I have to agree with objections given in the
referee reports. But, more important, I do NOT see any novelty in the
Paper. Your consideration of gauge degrees of freedom is well known
and similar considerations have been presented even in the papers of
my colleagues. The only novel thing, which you gave (and about which I
asked for an explanation), is the "unified" force equation. However,
I do not consider that your answer on my question is sufficient. So,
while your Paper is interesting, a serious revision (and extension)
is necessary for your Paper.
Valeri V. Dvoeglazov
Guest Editor
http://ahobon.reduaz.mx/~valeri/valeri.htm
Return-Path:
Received: from ahobon.reduaz.mx (ahobon.reduaz.mx [148.217.51.3])
by TheWorld.com (8.9.3/8.9.3) with ESMTP id MAA14400
for
Received: from ahobon.reduaz.mx ([148.217.51.54])
by ahobon.reduaz.mx (8.9.3/8.9.3) with ESMTP id LAA01482
for
Message-ID: <3BDEE8CD.20D61010@ahobon.reduaz.mx>
Date: Tue, 30 Oct 2001 11:52:14 -0600
From: Valeri Dvoeglazov
X-Mailer: Mozilla 4.61 [en] (Win95; I)
X-Accept-Language: en,ru
MIME-Version: 1.0
To: sweetser@alum.mit.edu
Subject: PS
References: <200110290218.VAA29927@world.std.com>
Content-Type: text/plain; charset=us-ascii
Content-Transfer-Encoding: 7bit
Valeri
To: Valeri Dvoeglazov
Reply-To: sweetser@alum.mit.edu
Subject: Re: PS
In-reply-to: Your message of "Tue, 30 Oct 2001 11:52:14 EST."<3BDEE8CD.20D61010@ahobon.reduaz.mx>
Date: Tue, 30 Oct 2001 13:19:19 -0500
From: Doug B Sweetser
Douglas Sweetser
Java
| The Bike | Lindy
Hop | Contact Doug